公開鍵暗号の仕組み

　量子コンピュータで暗号が解読されてしまうと言っても、それだけでは具体的に何が行われるのはわかりません。ひと口に暗号と言っても無数の種類がありますし、量子コンピュータといえども「この世界のあらゆる暗号を解読できる」というわけではないためです。

　そもそも、現時点で実用化されている量子コンピュータに暗号を解読する能力はほとんどありません。あくまで将来作られる汎用型量子コンピュータが、現在一般的に使われているいくつかの暗号を解読できるというだけです。

　その、「量子コンピュータに解読されてしまう恐れのある暗号」の1つがRSA暗号です。RSA暗号は世界的に広く使われている暗号で、私たちも普段から使っている一般的なものです。このRSA暗号は「公開鍵暗号」と呼ばれる「初めて会った相手と秘密の会話ができる」という特性を強みとして持っています。

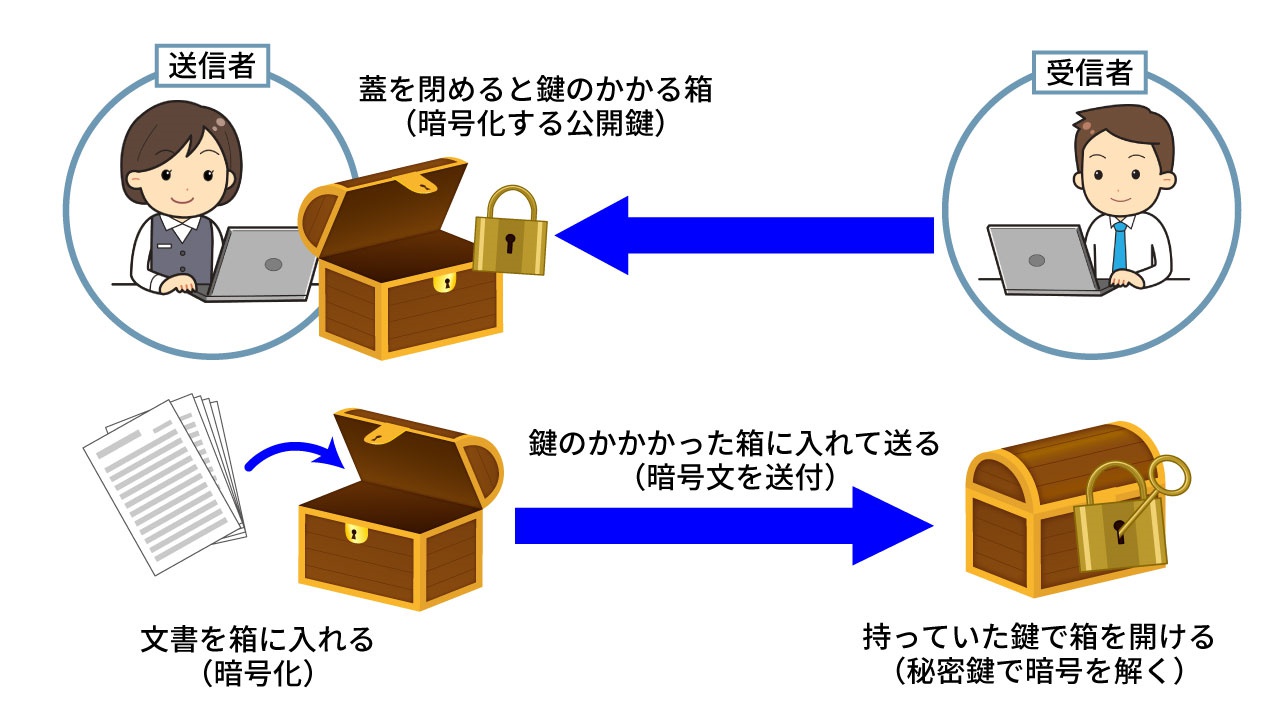
　これはなんてことのない特性に思われるかもしれません。しかし「鍵のかかっていない箱に入った荷物を、どうすればほかの人に取られないよう相手に届けるか」という問題を考えるとその難しさが理解できるのではないでしょうか。

　箱に鍵をかけてしまえば、受け手は鍵を持っていないため開けられません。先に鍵を送っても、途中で鍵を他人に取られてしまいます。そのため、鍵のかかった箱を後から送っても他人に取られた鍵で開けられてしまいます。

　解決困難な難問に思われますが、意外と簡単に解決できます。鍵を送るのではなく、（南京錠のように）錠前を閉めれば勝手に鍵のかかる箱を受け手に用意してもらいます。その上で、錠前を開けた状態の箱を受け手に送ってもらうのです。

　その箱に荷物を入れて錠前を閉めれば、荷物は誰に取られることもなく確実に相手に届きます。その箱の鍵は相手が持っているので、箱を開けることができるのはその相手だけだからです。

　このようにお互いに鍵のかかる箱を交換して、それに手紙を入れて送れば秘密の会話ができるようになります。これが「公開鍵暗号」と呼ばれる暗号です。


　公開鍵暗号は現代のITサービスが成立する上ではなくてはならない暗号で、私たちが安全にかつ手軽にインターネットを使えるのはこの暗号方式があるおかげです。

なぜ「現代の暗号」が解読されてしまうのか

　公開鍵暗号は誰とでも手軽に内緒話ができる一方で「鍵のかかる箱」を配っているため、箱についている錠前を詳しく調べることで鍵を作ってしまうことも可能です。そのため、公開鍵暗号では錠前を調べても簡単には鍵を作れないような仕組みになっている必要があります。

　コンピュータの世界ではこの箱と鍵の製作に数学的な手法を用いており、RSA暗号の場合は「因数分解」を使った暗号が利用されています。

　因数分解は「10＝2×5」のように、ある数字を素数同士の掛け算に置き換えるものです。この因数分解、一見単純なしくみですが、実はこの解を簡単に出す数学的手法は存在しません。基本的には素数で片っ端から割ってみて、その数字が割れるかどうかを1つ1つ確認していかなければ因数分解ができないのです。

　数字が小さければなんてことはありませんが、たとえば「3641527」を因数分解しろと言われたら困惑するのではないでしょうか。答えは「2963×1229」という2つの素数になるのですが、ここにたどり着くまでに何百回も割り算をしなければなりません。

　RSA暗号では、「因数分解を解くには何回も割り算をしなければいけない」という特性を利用して、数百桁の素数を使って暗号文を作っています。先ほどの例でいえば「3641527」が公開鍵（鍵のかかる箱）のようなもので「2963」「1229」は秘密鍵（箱を開ける鍵）と考えることができるでしょう。

　つまり、実際に使われている暗号の公開鍵は、因数分解によって数百桁の因数分解に成功すれば暗号が解けるというわけです。

　こう考えてみると、なんだかRSA暗号を使うのが心配になってくるのではないでしょうか。因数分解をすれば良いと言われると、なんだか簡単そうに思えてしまいます。

　しかしもちろん、実際の公開鍵にはスーパーコンピュータで何十年何百年かかるような大きな素数を使った鍵を使っています。ただ、そんな巨大な鍵は使いにくいので、公開鍵を使って使い勝手の良い「合鍵（共通鍵）」を送り、実際にはその合鍵で暗号通信を行っています。合鍵は公開されていないので解読するためのヒントがなく、受け渡しに気をつければ安全な鍵です。

　ただし、公開鍵が解読されると合鍵も盗まれてしまうので、合鍵に利用期限を設けます。公開鍵が解読される前に新しい公開鍵で別の合鍵を送り、何度も鍵を変えながら暗号通信を行っています。

　つまり、誰かに解読されたころには別の暗号を使っていることになり、因数分解をやり直して解読し直すハメになるので現時点で心配することはありません。

　しかしそれでも、高い計算能力を持つ量子コンピュータを使えば理論上は解読が可能になることがわかっています。では来たる量子時代、どのような暗号を使えば良いのでしょうか？

耐量子暗号として作られた「格子暗号」

　そこで生まれた、量子コンピュータを使っても解読できない暗号が「耐量子暗号」です。

　耐量子暗号にはいくつかの方式が考案されており、中でも応用範囲が広く安全性が高いのが「格子暗号」と呼ばれているものです。格子暗号は公開鍵暗号に対応しており、今まで通りに暗号を使ってインターネットを利用することが可能です。安全性も折り紙つきですが、その難解さは因数分解の比ではありません。

　「良くわからないけど安全らしいから量子時代も心配ない」と思えるなら良いのですが、安全であると言える理屈がわからなければ本当の意味で安心はできないでしょう。そこであくまで概念だけではありますが、次ページから簡単に解説をしてみます。

【次ページ】量子コンピュータの計算の仕組みは？「格子暗号」の概念を図解